Gaussian RBFNet: Gaussian Radial Basis Functions for Fast and Accurate Neural Fields Representation and Reconstruction

Anonymous Author(s)

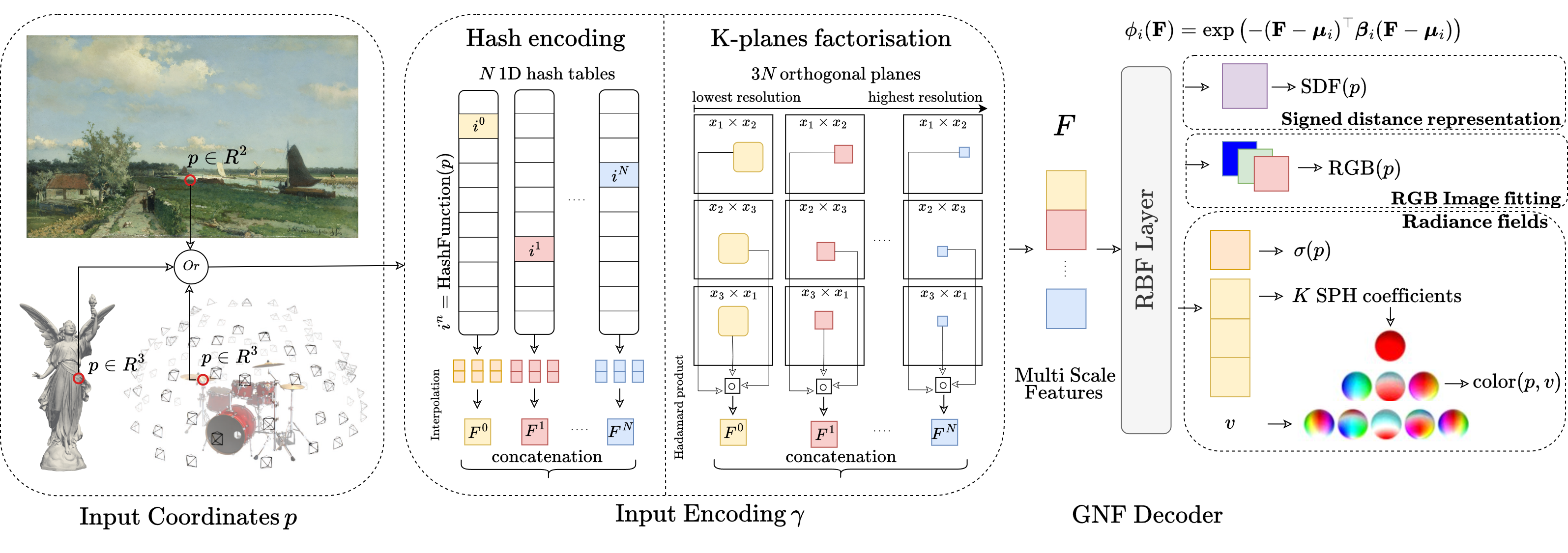
We introduce Gaussian RBFNet, a novel framework that leverages Gaussian Radial Basis Functions to represent neural fields efficiently. We demonstrate its effectiveness in representing 3D geometry, RGB images, and radiance fields.

Source Code Paper

Introduction

In this paper, we present a novel neural representation that is both fast in training and inference and lightweight. Our key insight is that traditional MLP neurons perform only simple computations, involving a dot product followed by a ReLU activation. Consequently, achieving complex nonlinear function representations usually requires shallow MLPs and high-resolution, high-dimensional feature grids. We demonstrate that by replacing traditional neurons with Radial Basis Function (RBF) kernels, our approach can accurately represent diverse signals, including 2D (RGB images), 3D (geometry), and 5D (radiance fields), using just a single layer of such neurons. Our proposed representation is highly parallelizable, leverages low-resolution feature grids, and offers a compact, memory-efficient solution.

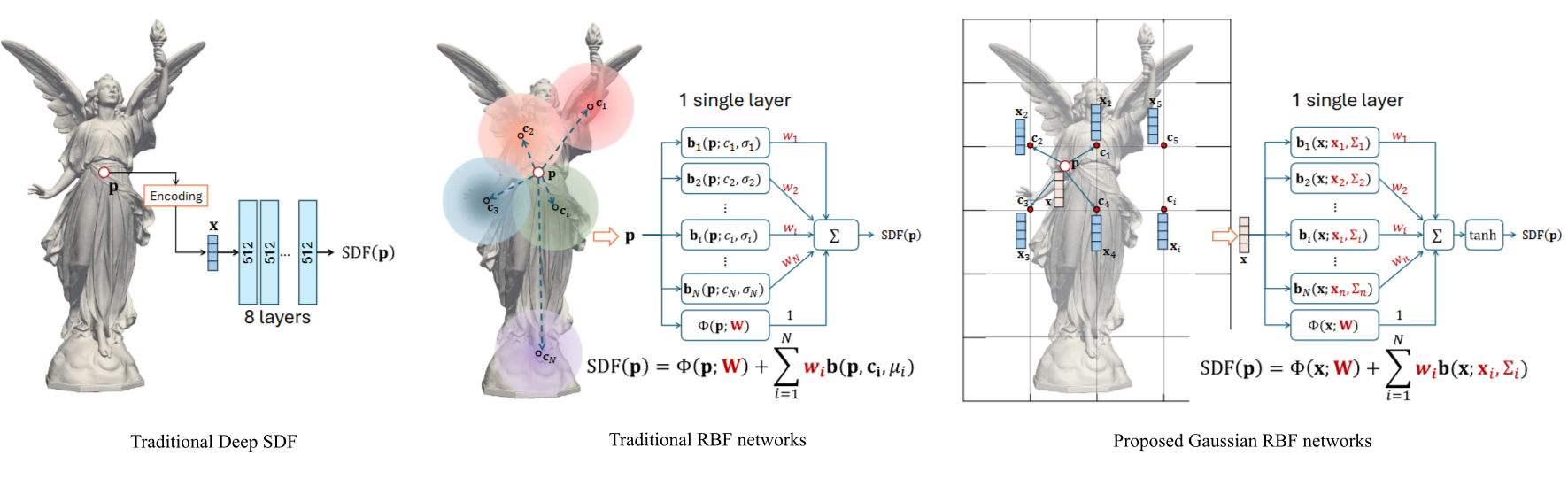
Our model (third figure from the left) stands out with its single decoding layer compared to other neural field models.

SDF Estimation

The following meshes represent the zero-level set of the SDF estimation obtained using our model and the DiF-Grid model from FactorFields. Our model uses approximately 3.5M parameters and converges in 15 seconds, whereas DiF-Grid has around 5M parameters and takes 20 seconds to converge.

Ultra-Fast Convergence!

The video below presents the extracted mesh during our model's training, with the training timer displayed in the bottom-left corner.

The overall shape is captured within a few seconds.

2D Images fitting

We use our model with a single RBF layer to fit high-resolution images. See examples below.

Zoom-in visualization of reconstructed images generated by our model.

Radiance Fields

We extend our framework to support a higher number of outputs, enabling the estimation of spherical harmonics for novel view generation. The proposed Gaussian RBF-SH model architecture is illustrated in the figure below.

Network architecture of the radiance fields model.

Novel views generated with our model.